Para que o sistema de simula??o microscópica reflita os fen?menos experimentais macroscópicos, é necessário replicar periodicamente o sistema de objetos simulados através de condi??es de contorno periódicas para evitar efeitos de borda que n?o existem na prática. Em princípio, o estudo teórico de qualquer sistema molecular requer a solu??o da equa??o de Schr?dinger dependente do tempo. No entanto, na prática, mais aten??o é dada à trajetória do núcleo. Tal trajetória pode ser obtida resolvendo a equa??o mecanica clássica do movimento usando a aproxima??o de Born-Oppenheimer. Alder e Wainwright disseram que os experimentos de simula??o por computador se tornar?o uma importante ponte conectando fen?menos experimentais macroscópicos e natureza microscópica. Após 10 anos de seus primeiros experimentos de simula??o de dinamica molecular, o físico francês Verlet prop?s um algoritmo de integra??o para as equa??es de movimento de Newton. Ao mesmo tempo, outro conjunto de algoritmos para gera??o e registro de pares de átomos vizinhos é proposto, o que simplifica bastante o cálculo da intera??o entre os átomos. Esses dois algoritmos ainda s?o amplamente utilizados na prática em algumas variantes [1, 2].

Uma variedade de métodos de simula??o em nível at?mico foi desenvolvida nas últimas décadas, incluindo estática de rede, dinamica de rede, Monte Carlo e dinamica molecular. Entre eles, a dinamica molecular é especialmente adequada para o estudo da deforma??o plástica. Estuda o comportamento em tempo real do processo de deforma??o através da solu??o da equa??o de Newton do sistema de intera??o at?mica de algumas fun??es de potencial de intera??o interat?mica definidas, e inclui a n?o simplifica??o da rede. Harmonicidade, desnível de altura de estresse interno e resposta transitória do sistema.

A dinamica molecular depende principalmente da mecanica newtoniana para simular o movimento do sistema molecular para extrair amostras de sistemas compostos de diferentes estados do sistema molecular, calculando assim a integral de configura??o do sistema e calculando ainda mais o sistema com base nos resultados da configura??o integrante. Grandezas termodinamicas e outras propriedades macroscópicas. Ele resolve a equa??o de movimento para um sistema multicorpos composto de núcleos e elétrons. é um método computacional que pode resolver o problema de dinamica de sistemas de um grande número de composi??es at?micas. Ele pode n?o apenas simular diretamente as características de evolu??o macroscópica de uma substancia, mas também concordar com os resultados do teste. Cálculos semelhantes também podem fornecer uma imagem clara da microestrutura, movimento de partículas e sua rela??o com propriedades macroscópicas, fornecendo suporte técnico poderoso para o desenvolvimento de novas teorias e conceitos.

O objeto da dinamica molecular é um sistema de partículas. A intera??o entre os átomos no sistema é descrita pela fun??o potencial. Portanto, a sele??o correta do tipo de fun??o potencial e seus parametros desempenha um papel importante nos resultados da simula??o. Na maioria dos casos, a fun??o de energia potencial simplifica a descri??o da deforma??o geométrica da molécula na medida em que apenas o termo harm?nico simples e a fun??o trigonométrica s?o usados; em vez da intera??o entre os átomos de liga??o, apenas a intera??o de Coulomb e o potencial de Lennard-Jones s?o usados. Combinado para descrever. Entre eles, a descri??o da for?a de intera??o entre os átomos é geralmente empírica ou semi-empírica, o que pode melhorar a eficiência computacional, mas n?o pode revelar completamente as propriedades multicorpos da liga??o eletr?nica, especialmente as complexidades relacionadas à sua estrutura e química em proximidades dos defeitos. Fun??o variacional autoconsistente. A fun??o potencial EAM (embedded-atom model) de Daw e Baskws combina as propriedades multicorpos da liga??o eletr?nica até certo ponto.

A confiabilidade da fun??o potencial depende principalmente da precis?o dos parametros do campo de for?a, e os parametros do campo de for?a podem ser obtidos ajustando dados de observa??o experimental e dados ab initio de mecanica quantica. Atualmente, o campo de for?a molecular mais utilizado na simula??o de sistemas macromoleculares biológicos é o campo de for?a CHARMM e o campo de for?a AMBER, que é o campo de for?a molecular para o estudo inicial de macromoléculas biológicas. Os parametros de campo de for?a existentes ainda est?o sendo continuamente otimizados e os tipos de moléculas cobertas também est?o se expandindo. O modelo de granula??o grossa vem ganhando cada vez mais aten??o na pesquisa biofísica computacional, uma vez que partículas granuladas grosseiras s?o definidas neste modelo, correspondendo a vários átomos ou grupos at?micos ou mesmo moléculas no modelo de todos os átomos. O número de partículas no sistema é reduzido, de modo que a escala de tempo e espa?o da simula??o pode ser bastante melhorada, mas os detalhes at?micos também ser?o perdidos. Simula??es de dinamica molecular baseadas neste modelo s?o adequadas para estudar fen?menos biológicos lentos ou fen?menos biológicos que dependem de grandes montagens.

O princípio fundamental de projetar um campo de for?a básico é minimizar a sobrecarga de energia computacional em um intervalo de tempo para maximizar a escala de simula??o. Isso é especialmente importante para o campo de for?a at?mico completo, mesmo para o chamado modelo de granula??o grossa. Em particular, esse princípio é extremamente importante se você deseja simular escalas de tempo de microssegundos ou mesmo milissegundos.

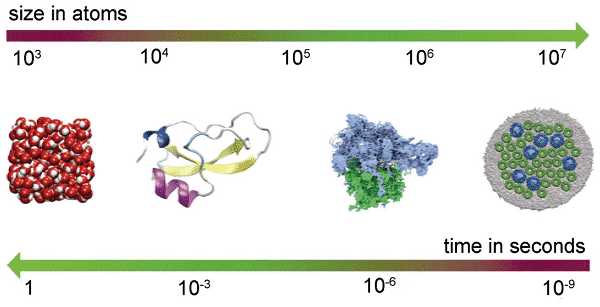
A Figura 1 mostra a rela??o inversa entre as dimens?es de tempo e espa?o da dinamica molecular, da esquerda para a direita na figura: (1) água, os componentes básicos das células; (2) inibidor de tripsina bovina, uma enzima, que "o comportamento respiratório pode ser examinado em uma escala de milissegundos; (3) ribossomos, um dispositivo biológico complexo que pode decodificar informa??es genéticas e produzir proteínas; (4) fragmentos de membrana fotossintética bacteriana roxa, com 25 milh?es de átomos, a figura mostra o complexo de capta??o de luz embutido na bicamada fosfolipídica e no centro de rea??o fotoquímica.

Figura 1 Rela??o de escala entre tempo e espa?o da dinamica molecular clássica

Com o rápido crescimento dos processadores de computador e o desenvolvimento de arquiteturas de computa??o massivamente paralelas, a combina??o de técnicas de arquitetura massivamente paralelizadas ou proprietárias com programas de dinamica molecular escaláveis, as simula??es de computador variam de deslocamentos a mecanismos de deforma??o baseados em limites de gr?os. Toda a gama de tamanhos de gr?os abre novos caminhos para explorar as fronteiras de pesquisa de sistemas de materiais.

Por exemplo, William Gon?alves et al. utilizou a fun??o potencial Wolf BKS (van Beest, Kramer e van Santen) para descrever a intera??o entre os átomos, usando o simulador paralelo at?mico/molecular de grande escala LAMMPS (Large-scale Atomic/Molecular Massively Parallel). Simulator) estudou a dinamica molecular da elasticidade e resistência de aerogéis de sílica. Eles usaram o algoritmo de velocidade-Verlet e passo de tempo de 1,0 fs, e usaram condi??es de contorno periódicas em todas as três dire??es.

A Figura 2 é um diagrama esquemático 3D de uma amostra de grande volume simulada de mais de 7.000.000 átomos e uma se??o de amostra de 20 nm de espessura e uma vis?o parcial ampliada (azul é um átomo de oxigênio, vermelho é um átomo de silício) e a Figura 3 (a ) é um aerogel de 803 nm 3 . A amostra foi submetida a um teste de tra??o uniaxial para obter uma curva tens?o-deforma??o de 300 K, (bd) é uma imagem típica de fratura dúctil, e (e) uma rela??o logarítmica entre resistência à tra??o e volume da amostra. Eles analisaram que, para garantir a avalia??o adequada de propriedades mecanicas, como elasticidade, o tamanho da amostra simulada é pelo menos 8 vezes o tamanho do poro, enquanto o aerogel de sílica com uma altura de superfície positiva requer uma taxa de deforma??o relativamente baixa para garantir quase condi??es estáticas.

Figura 2 Amostra de aerogel de sílica simulada (mais de sete milh?es de átomos)

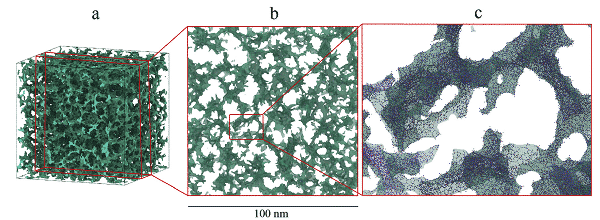
Fig. 3 Curva tens?o-deforma??o (a), rela??o for?a-volume (e) e imagem de fratura (bd) do teste de tra??o uniaxial

Geralmente, o tamanho de gr?o crítico dc é cerca de 20-30 nm, e a maior deforma??o para o tamanho de gr?o (50-100 nm) é determinada principalmente por discordancias; quando o tamanho de gr?o é inferior a 30 nm, é dominado principalmente pelo processo de deforma??o GB, e o tamanho de gr?o é reduzido. Isso resulta em uma diminui??o na resistência e tens?o de fluxo, ou seja, um "efeito anti-Hall-Petch". No entanto, a extensa compara??o entre potenciais multicorpos e pares usados para modelar GBs em metais fcc e bcc revela que há pouca diferen?a qualitativa no comportamento previsto por essas diferentes descri??es de for?a, sugerindo que os efeitos multicorpos podem n?o dominar o comportamento GB.

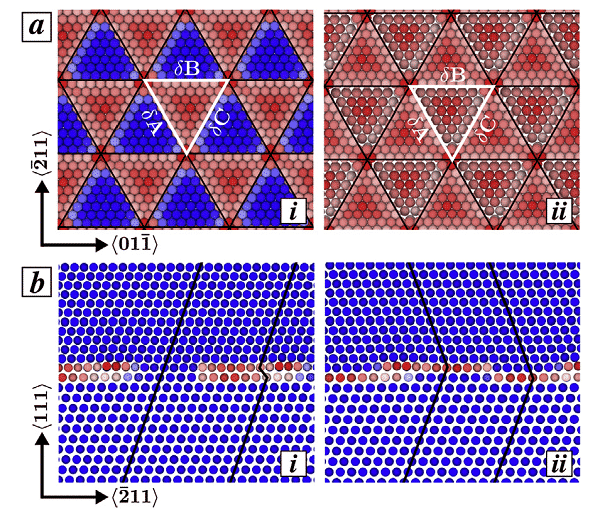
Bejaud, J. Durinck et ai. usaram simula??o de dinamica molecular para estudar a intera??o entre gêmeos deformados e interfaces Cu/Ag nanoestruturadas, e analisaram os efeitos da estrutura da interface na nuclea??o, expans?o e espessamento de gêmeos, e explicaram a interface de incompatibilidade. O papel da grade de deslocamento. A Figura 4 mostra a grade de deslocamento parcial de Shockley (destacada por linhas pretas), o padr?o triangular (se??o branca) e a distribui??o de falhas de empilhamento na interface. Entre eles, o átomo é colorido de acordo com o parametro de simetria central, o átomo azul está no ambiente FCC perfeito e o átomo vermelho está na falha de empilhamento ou na falha de gemina??o.

Figura 4 (a) Vista superior dos átomos de Cu e Ag ao longo da interface: (ai) interface COC, (a.ii) interface TO, (b) vista lateral ao longo da dire??o X = <011>: (bi) em COC No interface e o caso, a regi?o coerente alterna com a regi?o de falha de empilhamento inerente (ISF), (b.ii) a interface TO, e a regi?o de defeito duplo existe continuamente na camada de Cu e na camada de Ag.

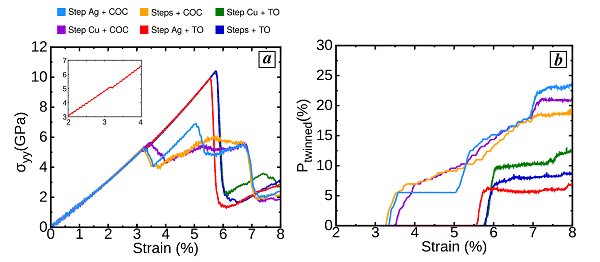
A Figura 5 mostra a curva tens?o-deforma??o e a raz?o at?mica dos gêmeos em fun??o da deforma??o. Através de análises, eles descobriram que a interface pode induzir direta ou indiretamente a nuclea??o de discordancias gêmeas através de discordancias de Lomer, e como a estrutura da interface heterogênea afeta as diferentes etapas do processo de gemina??o mecanica, afetando assim a forma??o de tantalo no Cu/Ag nanoestruturado. O tamanho do cristal. Este método de escala at?mica fornece algumas bases teóricas úteis para o processo de gemina??o mecanica em compósitos em nanoescala.

Figura 5 (a) curva tens?o-deforma??o, (b) raz?o at?mica de gêmeos em fun??o da deforma??o

Projetar materiais multicamadas para ajustar as propriedades mecanicas é um tópico importante ao controlar o mecanismo de deforma??o porque a gemina??o permite a incorpora??o de propriedades mecanicas de nanocamadas e materiais nanocristalinos. A este respeito, este estudo fornece a chave para a compreens?o do mecanismo da intera??o de interface dupla e apoia a vis?o de que as interfaces heterofásicas promovem a gemina??o.

Para compósitos em camadas de escala ultrafina contendo metais estruturais hcp de baixa simetria, um grande número de heterointerfaces pode efetivamente absorver defeitos como vacancias e átomos intersticiais causados por irradia??o nuclear, e os próprios metais hcp têm baixa densidade, for?a específica e nos últimos anos , materiais multicamadas hexagonais compostos de Ti, Zr, Mg e outros metais come?aram a atrair a aten??o das pessoas devido à sua alta rigidez específica e boa condutividade elétrica e térmica. No entanto, em compara??o com os metais fcc e bcc com alta simetria da estrutura cristalina, o metal hcp tem baixa capacidade de deforma??o plástica à temperatura ambiente, o que restringe o uso de materiais compósitos relacionados.

Além da resolu??o espacial e temporal da escala at?mica, a simula??o de dinamica molecular pode descrever o comportamento do modelo de nanocristal idealizado totalmente caracterizado, como estrutura interfacial, for?a motriz e mecanismo at?mico; por outro lado, pode estar em contornos e posi??es de gr?o muito altos. O grande comportamento de deforma??o plástica foi observado na densidade errada. Por exemplo, mecanismo de nuclea??o de deslocamento, têmpera de contorno de gr?o, gemina??o mecanica em Al nanocristalino, redu??o do tamanho de gr?o de deslocamento para mecanismo de deforma??o baseado em contorno de gr?o, observa??o de banda de cisalhamento e sua rela??o de superfície de fratura.

Além disso, na aplica??o prática e no processo de pesquisa, o modelo teórico para diferentes descri??es e sele??es de problemas, a dinamica desenvolveu muitos ramos teóricos, por exemplo, Jian Han, Spencer L. Thomas da Universidade da Pensilvania e outros contam com o poder da fronteira A descri??o da desconex?o resume o conceito de dinamica de contorno de gr?o de materiais policristalinos, Zheng Ma et al. estudaram a cinética de precipita??o do FeCO3, bem como a cinética de superfície/interface.